The inverse of a right-continuous non-decreasing function appears a lot in probability. I used to have a hard time to remember the precise form of it. Here is a little digging into this problem.
The inverse of a right-continuous non-decreasing function can be defined in two ways: \[F^{-1}(w) = \sup\{ y: F(y) \leq w\} \quad \text{or} \quad F^{-1}(w) = \inf\{y: F(y) > w\}\]
The inverse of a left-continuous non-decreasing function can be defined in two ways: \[G^{-1}(w) = \sup\{ y: G(y) < w\} \quad \text{or} \quad G^{-1}(w) = \inf\{y: G(y) \geq w\}\]
The equality makes a lot of differences, because the equality affects if the inverse of inverse function is the original value. Drawing a picture is helpful to remember the correct form of them.
Right-continuous:
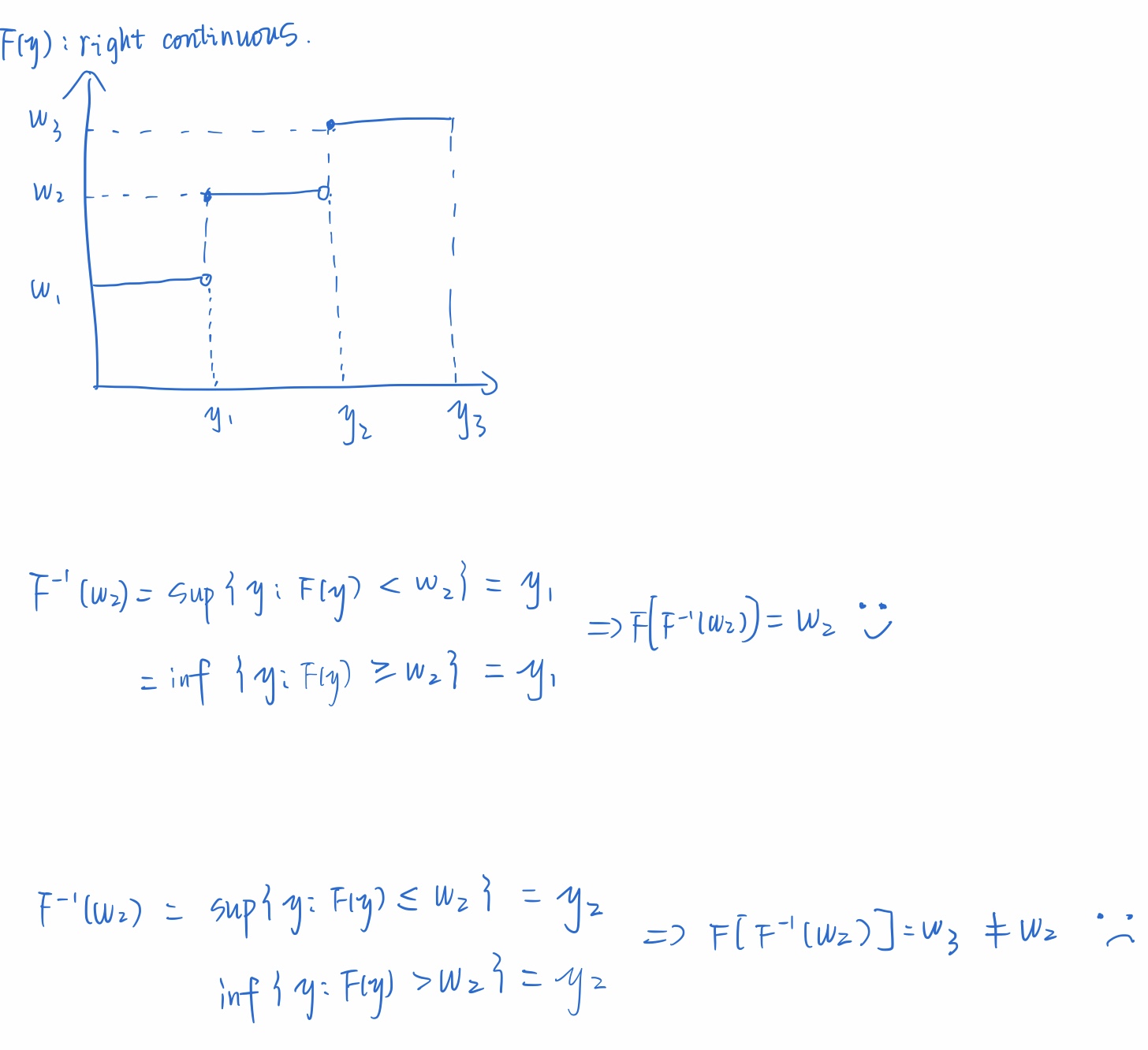
Left-continuous:
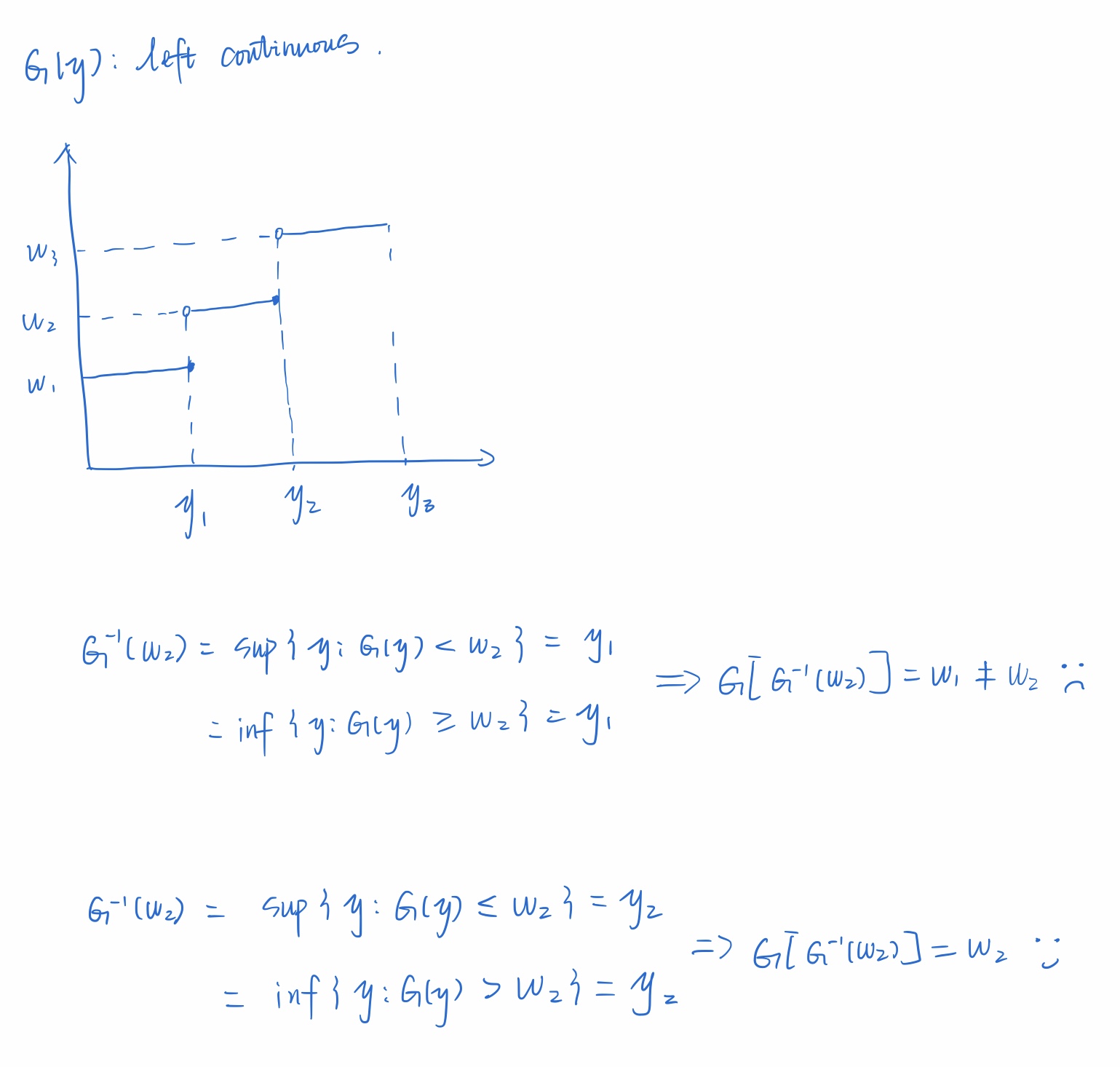
Moreover, if the function is continuous, all the four expressions
\[H^{-1}(w) = \sup\{ y: H(y) < w\}\quad \text{or} \quad H^{-1}(w) = \inf\{y: H(y) \geq w\}\] \[H^{-1}(w) = \sup\{ y: H(y) \leq w\} \quad \text{or} \quad H^{-1}(w) = \inf\{y: H(y) > w\}\] are valid, because they all satisfy \[H(H^{-1}(w)) = w\]